Statistics ? Descriptive statistics Vs Inferential statistics
Statistics
Statistics is often known as one of the most versatile and useful areas of Mathematics. It helps us to make educated guesses about the unknown and find very useful information in this very ocean of data. But despite all this usefulness, many people struggle to understand this statistic. What is this statistics and how does it work ?
Statistics if its misapplied because of poor understanding of this concept can lead to some false conclusion, so that is why understanding and applying statistics become utmost important. Some of the best examples could be keeping track of your favorite football team or try to predict the outcome of an election through exit polls.
Statistics play very important role in some critical decision-making situations. Statistics help us make sense of the vast amount of information in the world as through see though your eyes and listed through your ears, you can filter out vast number of unnecessary stimuli which may not be useful to us.
What Statistics means to you may be different for someone else. Take an example scientist use statistics on daily basis to predict the weather forecast for each and every day. Statistics is all about making sense of data collected and analyzing, interpreting, and then figuring out how to put that information to best of use. Today, in this blog, we’re going to answer all these questions.
Let’s understand this in simple language.
Statistics come from word “Statista” which is an Italian word which means any statement It came in to picture somewhere in 1660. It was first discovered by Gottfried Achenwall, who was a German philosopher, economist and one who invented the statistics. He is also known as “Father of Statistics”.
Later on Sir John Sinclair popularized this concept to even further heights. Statistician is person who use statistical tool and techniques to interpret data. Sir Ronald Aylmer Fisher contribution to this field of statistics was immense hence he is known ad “The Father of Modern Statistics”. He worked on Design of Experiments.
📚 Not sure which book to choose?
Statistics All-in-one Dummies : Click here to Buy from Amazon
Statistics Essentials For Dummies : Click here to Buy from Amazon
Statistics is a branch of Science which deals with collection, analysis and interpretation of data.
To be more specific statistics can be broken down into the two main areas :
- Descriptive Statistics
- Inferential Statistics
Descriptive Statistics
Descriptive statistics makes use of the data to provide brief descriptions of the population, either through numerical calculations or graphs or tables. The main purpose of this type of statistics is present data in a way that will help in describing the data with help of Graphs to facilitate easy understanding.
Descriptive statistics make the data we get more easy to digest, even though we may lose some information about individual data points. Descriptive Statistics is all about summarizing or highlighting most important aspects of our data that we have collected. When people think of statistics, they often think about this descriptive statistics i.e. this area.
The tools here are about describing the information you have collected and then defining the task such as using a tools like graph or calculating a simple average with descriptive statistics
Inferential Statistics
Inferential statistics makes good inferences and near perfect predictions about a population based on a sample of data taken from the population. Inferential statistics help us make decisions about data’s uncertainty.
Inferential Statistics helps in making predictions from our data. So in Inferential Statistics the goal is to take just a small bit of information, analyze it thoroughly, and then see what conclusions we can draw based on available information or infer about the bigger picture for future.
This part of statistics is most enigmatic, but in actual certainty, it is one of the most powerful tool and it allows us to find even more information from the data that we have already collected.
Let’s understand the difference between these two with help of an example:
Suppose you are evaluating average marks scored by Class 7A in Science subject. Since you are evaluating the performance of Class 7A only using the data that you have collected either through numerical calculations or graphs or tables and are not making any generalized conclusion about other batches of class 7. This is called Descriptive statistics.
Now you decide that based on this data of Class 7A, I want to estimate the average marks in all other sections of Science. Now this way of estimating we call it Inferential Statistics. So, any conclusion or inference that we can draw from this data tell us how that data would be. Statistician call it Statistical Inference.
Categories of Descriptive Statistics :
Descriptive statistics often categorized as
- Measure of Central Tendency
- Measure of Spread
- Measure of Shape
Categories of Inferential Statistics :
- Confidence Intervals ( YouTube video link)
- Test of Significance Or Hypothesis Testing
Measure of Central Tendency
In Descriptive statistics, central tendency (or measure of central tendency) which is a single point middle value describing data set by identifying its Mean, Median and Mode. Measure of central tendency gives the location. Measure of Central tendency is also known by another name “Measure of Location“. Click this YouTube video link for detailed understanding.
Mean
Average of all values. Most popular measure of descriptive statistics. Say for examples we have n values of data having individual values as A1, A2, A3….An . Then mean or arithmetic mean is calculated as A1+ A2+ A3+….An/ n.
Assume the following data set : 10,20,30,20,40,20,10
Sum = 10+20+30+20+40+20+10 = 150 ; N= 7
Mean = 150/7 = 21.42
The mean of these data is 21.42
Median
First thing , we need to arrange the data in ascending order.
– If number of value is ODD, then the median is the middle value when arranged in ascending order.
– Is number of value is EVEN, the median is the average of two middle value when arranged in ascending order.
Assume the following data set : 10,20,30,25,40,35,10
Arranging in ascending order : 10, 10, 20, 25, 30, 35, 40
Median is 25 (Since number of value is “Odd”)
Lets take another example when data set is “Even”
Assume the following data set : 10,20,30,25,40,35,10, 20
Arranging in ascending order : 10, 10, 20, 20, 25, 30, 35, 40
Median is 20+25/2= 22.5 (Since number of value is “Even”)
Mode
Most frequent occurring value in a set of data values
Assume the following data set : 10, 20, 30, 20, 40, 20,10
Most frequent occurring value =20
Measure of Spread
Measure of Spread is also known by another name “Measure of Dispersion“. It defines how the data is spread or scattered.
Assume the following data set : 49, 50, 58, 58, 60, 62, 66, 68, 70, 72
•Average = 61.3
•Range: R = max – min. = > = 72- 49 = 23
•Variance: The standard deviation is simply the positive square root of the variance
•Standard Deviations: The standard deviation is simply the positive square root of the variance
Measure of Shape
Measures of shape describe how the data is distributed. Measure of Shape is further categorized in to two types : Symmetry and Modality
Skewness
Skewness measures spread of data, whether its symmetrical or skewed to Left or Right. If it is skewed to the right it is called Positive Skewed and if it the left it is called Negative Skewed. Skewness measures typically range from -3 to +3. Skewness vale of “0” is considered “Normal” .
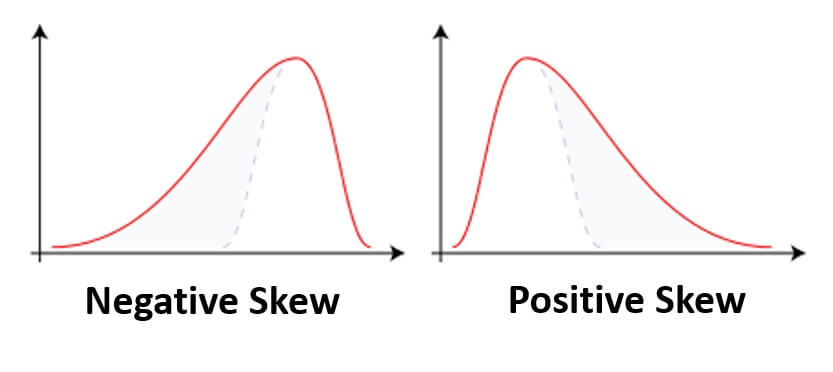
Symmetric : Mean=Median=Mode ( Normal Distribution )
Left skewed : Mean<Median
Right skewed : Median< Mean
Kurtosis :
Kurtosis measures peak of data. whether its heavy tail or light tail. Kurtosis measures typically range from -3 to +3. Kurtosis value of 3 denotes normal distribution. Normally 3 types of kurtosis are there : Mesokurtic, Leptokurtic and Platykurtic.
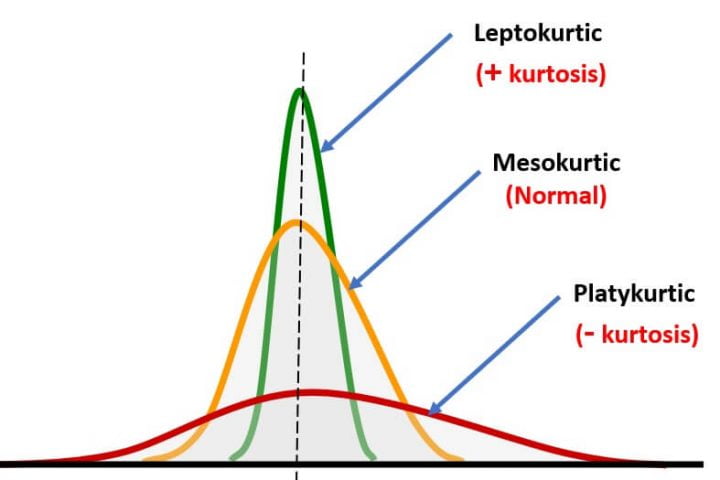
Mesokurtic:kurtosis value = 3 ( Normal Distribution )
Leptokurtic: kurtosis value > 3
Platykurtic: kurtosis value < 3
Modality
Unimodal : Distribution with single peak
Bimodal Distribution with two peak
Multimodal : Distribution with more than two peak
I hope this blog helped in understanding the basic concept in a simplified manner, watch out for I hope this blog helped in understanding the basic concept in a simplified manner, watch out for more such stuff in the future.
📢📢 𝑺𝒐𝒄𝒊𝒂𝒍 𝑴𝒆𝒅𝒊𝒂 𝑳𝒊𝒏𝒌:
Thanks!!!
For questions please leave them in the comment box below and I’ll do my best to get back to those in a timely fashion. And remember to subscribe to Digital eLearning YouTube channel to have our latest videos sent to you while you sleep.
✍️ 𝓓𝓲𝓼𝓬𝓵𝓪𝓲𝓶𝓮𝓻: Copyright Disclaimer under section 107 of the Copyright Act of 1976, allowance is made for “fair use” for purposes such as criticism, comment, news reporting, teaching, scholarship, education and research. Fair use is a use permitted by copyright statute that might otherwise be infringing. The information contained in this video is just for educational and informational purposes only and does not have any intention to mislead or violate Google and YouTube community guidelines or policy. I respect and follow all terms & conditions of Google & YouTube.
