Confidence Interval in Statistics | How to find a 95% Confidence Interval ?

Before we understand the confidence Interval, let us first understand what do we mean by “Estimate“. Everyone makes some kinds of estimates at some point of time in their life. Imagine that you are crossing the road, and you see the car that is approaching you fast and now you can estimate the speed of that same car that is approaching you. Based on this estimate you can make your decision if you to wait, walk or run. This is called Estimate.

Now let’s define the Estimate in statistical terms. Estimate is a specific observed numerical value used to estimate an unknown population parameter or gives you some facts about how the population could be. We can have two types of estimates about the population.

Point Estimate and Interval Estimate :

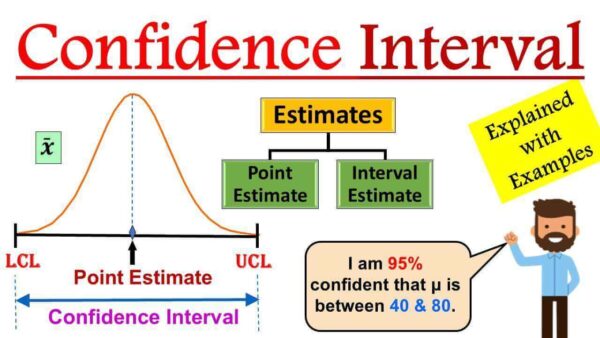
Point Estimate

Suppose we have some population and we take a sample from this population and measure their weights estimate mean.

Average weight is 60 Kg. Then 60 kgs of sample mean is a Point estimate of a population mean.

Point estimate is often insufficient because its is either wrong or right.  Assuming that we know its is wrong, but you don’t know how wrong it it. And you cannot be certain of estimate reliability. Assuming we came of know that you are off target by 5 kg, then you would expect 60k as good estimate but if the estimate is off by 30kg then it is not the right estimate of population.

Also the point estimate is going to be different from the population parameter because due to the sampling error, and there is no way to know who close it is to the actual parameter. For this reason, statisticians like to give an interval estimate which is a range of values used to estimate the parameter.

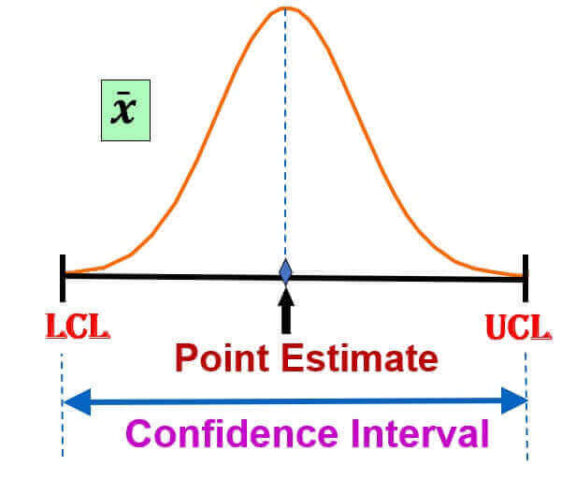
Interval Estimate

Because a point estimates is a single value, we can’t really tell how good it represents the population. So in inferential statistics, we prefer to use an interval or a range of values to estimate the population parameter. It gives you the range of values by calculating two different numbers between which we can expect the parameter to lie. So we construct Interval estimate with degree of certain degree of confidence say for e.g. 95% confidence.

Confidence Interval

Confidence interval is the range of estimate we are making.

Don’t confuse confidence interval with confidence levels. Confidence levels are normally expressed as % ( For e.g. 95 % confidence level).  A confidence interval communicates how accurate our estimate is likely to be. We use a confidence interval to express the range in which we are pretty sure the population parameter lies. These confidence Interval give us an idea about the size and thus the power of a study. 

The size of the confidence interval is then directly related to the size of the study. The more participants the smaller the confidence interval and the more precise the estimated effect.  In essence, the confidence interval estimate for a population mean lies between the sample mean – the margin of Error and the sample mean + the margin of Error.

The margin of error is calculated based on a confidence level. The confidence level basically refers to the percent of confidence intervals (from many samples) that we expect to contain the true population parameter. 

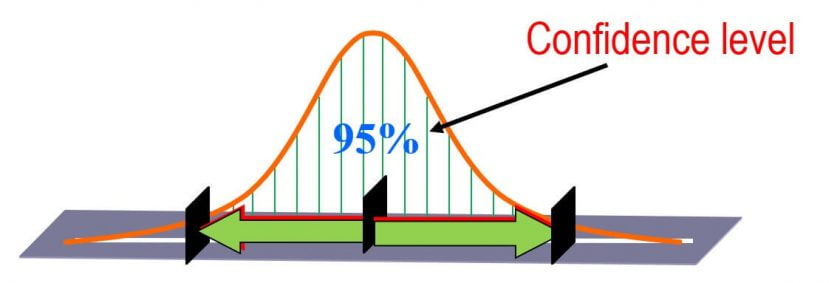
Confidence levels of 90%, 95%, and 99% are often used, but 95% is the most commonly used confidence level. Most of times confidence intervals can be found using the t-distribution (When you are working with smaller number of samples.

Say for e.g we are 95 % confident that True mean will lie between 40 and 60. It indicates the error in two ways one by the extent of its range and other by probability of true population parameter lying within the range. Interval Estimates of population parameters are often called Confidence Intervals.

So 95% confidence interval is a range of values that you can be 95% certain contains the true mean of the population. The correct interpretation of a 95% confidence interval is that “we are 95% confident that the population parameter is between 50 and 70.”

Inference is when we draw conclusions about the population from the sample. Because the sample was only a selection of objects from the population, it will never be a perfect representation of the population.

Confidence Interval is the most common type of interval estimate is made of two elements :

Confidence Interval = “Point estimate” +/- “Margin of Error”

Where Margin of errors are the upper and Lower limits of confidence Interval.

Now we can think let’s choose high confidence level say for e.g. 99% in all your estimation. But in practice, high confidence levels will produce large confidence intervals and they will end up giving very different estimates. Statisticians prefer interval estimate over point estimate because interval estimate are often accompanied with degree of confidence.

——————————————————————————————————————————————————-

Let’s understand this with some Scenarios:

Scenario #1

John : Will I get my Television within 1 year ?

Manager : I am absolutely certain that you will get in 1 year

Confidence level : Better than 99%

Confidence Interval : Would be 1 year

Scenario #2

John : Will I get my Television within 1 month ?

Manager : I am absolutely positive that you will get in 1 month

Confidence level : Better than 95%

Confidence Interval : Would be 1 month

Scenario #3

John : Will I get my Television within 1 week ?

Manager : I am positive that you will get in 1 week

Confidence level : Better than 80%

Confidence Interval : Would be 1 week

Scenario #4

John : Will I get my Television within 1 day ?

Manager : I can try that you will get in 1 day

Confidence level : Better than 30%

Confidence Interval : Would be 1 day

Scenario #5

John : Will I get my Television within 1 Hour ?

Manager : I can try but highly unlikely that you will get in 1 hour

Confidence level : Better than 5 %

Confidence Interval : Would be 1 hour

——————————————————————————————————————————————————-

Let’s understand this with some examples:

Example 1 : CI for Single population Mean

A random sample of n = 50 males showed a mean average daily intake of dairy products equal to 756 grams with a standard deviation of 35 grams.  Find a 95% and 99% confidence interval for the population average U ? 

Ans: x ̄ = 756 grams ; n= 50 , σ = 35 ,

The Z-value can be derived from the table and its shows us which area is contained in the confidence interval of our result so in case of the 95% confidence interval we take although use between minus 1.96 times and plus 1.96 times the standard deviation. A lower confidence interval will lead to a lower Z-value and a smaller interval and vice versa

From Z table for 95 % confidence interval we get value as 1.96.

 => Interval estimate is = 756±1.96×35/√50

 => 746.30 ≤ m ≤ 765.70 grams  for 95 % confidence interval

Now for 99 % confidence interval and From Z table for 99 % CI we get value as 2.576

=> 756±2.576×35/√50

=> 743.23 ≤m≤ 768.77 grams  for 99 % confidence interval.

——————————————————————————————————————————————————-

Example 2 : CI for Single population Proportion

Billing statement for 1000 patients discharged from a particular hospital were randomly selected for error. Out of 1000 billing statements, 102 were found to contain errors. Using this formation lets construct 99% confidence interval ?

Ans: p ̂ = 102 / 1000 = 0.102

From Z table for 99 % confidence interval we get value as 2.576

p ̂ =  is random and varies from sample to sample

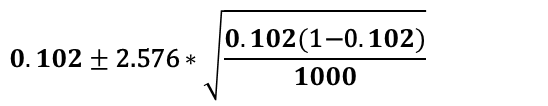
0.077 ≤p ̂≤0.127for 99 % confidence interval

——————————————————————————————————————————————————-

Watch this YouTube video for detailed explanation :

For questions please leave them in the comment box below and I’ll do my best to get back to those in a timely fashion. And remember to subscribe to Digital eLearning YouTube channel to have our latest videos sent to you while you sleep.